Final Project – Conditional Probability
Introduction
In this course, we will discuss the definition of conditional probability and its application to solving real-world problems. Probability is a central concept in mathematics used to quantify the likelihood of uncertain events occurring. It is used extensively in the UVic courses MATH 151 and STAT 252. The concept of probability originated in the 17th century and evolved with the study of gambling problems (Literature Cited).
In addition, probability has important applications in fields such as science, engineering, and business. For example, with conditional probability, we can analyze the outcome of rolling dice or drawing playing cards to make data-driven decisions.
Learning Outcomes
- Understand the definition and apply the formula of conditional probability.
- Distinguish between dependent and independent events
- Describe at least one industry’s Application of Conditional Probability in Real-Life Situations.
Read and Watch
https://www.mathsisfun.com/data/probability.html (15min) – Demonstrates the concept of the probability basic rules
https://doi.org/10.1007/978-1-4612-4374-8 – (20 min) The use of probability
Concept
Definition of Conditional Probability
Definition of Conditional Probability: Conditional probability describes the probability of another event occurring when an event is known to have happened. The formula is as follows:
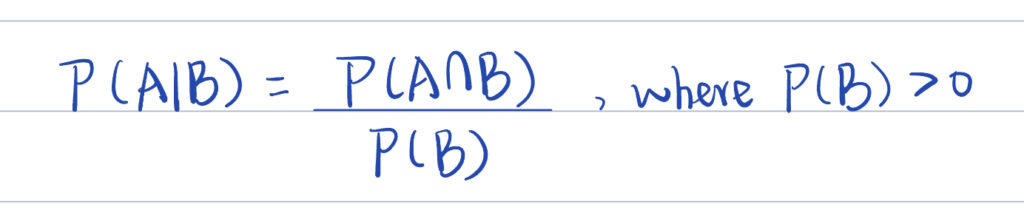
Where:
- P(A∣B) is the probability of event A occurring under the condition that event B occurs.
- P(A∩B) is the probability that event A and event B occur simultaneously.
- P(B) is the probability that event B occurs.
Example:
Prerequisite: There are 60 students. 30 students take math, 20 students take physics, and 15 students take both subjects.
Question: Given that a student takes physics, what is the probability that they also take math?
Solution:

Dependent & Independent Events
Dependent Events: Two events are dependent if the occurrence of one affects the probability of the other.
Formula:

Example of a Dependent Event:
Independent Events: Two events are independent if the occurrence of one does not affect the probability of the other.
Formulas:

Example of an Independent Event:
Venn Diagrams:

We can also use Venn diagrams to distinguish between Dependent events (intersecting) and Independent events (non-intersecting).
Part III: Practical Applications and Importance of Conditional Probability in Real Life
Conditional probability is a very important concept in mathematics and it has many wide applications in real life. Through conditional probability, we can analyze data and future directions based on in known conditions. I will explain the application of conditional probability in mainstream scenarios in order to help you better understand the application of conditional probability in life.
Medical field
First of all conditional probability plays a very important role in disease detection and diagnosis.
For example, there is a disease test with a positive rate of 95%, but only 1% of people are actually infected with the disease. By using conditional probability, we can calculate the probability that people will actually get the disease if they test positive, which helps doctors to make a diagnosis and reduce misdiagnosis.
Risk management
Second, insurance and financial companies can use probability to help them assess risk.
For example, insurance companies can calculate the likelihood that a customer will get sick based on their health status and lifestyle habits. This can help them calculate the cost of insurance for different groups of people.
Machine learning
Conditional probability is one of the foundations of recommendation algorithms and classification models.
For example, in our commonly used e-commerce platforms predict the items that users may like based on their search history and purchase history before displaying them on the customer’s homepage. E-commerce platform based on the condition that the user has already purchased a certain product, and then go to calculate the probability of purchasing other related products.
Assessment
Learning Activity
Have students cut two large circles out of colored cardstock:
- The blue circle represents the 80 households that have pets
- The yellow circle represents the 50 households that have gardens
Draw a large box on the board to represent 120 households and have students come up to the table and place the two circles:
- The overlapping part of the two circles is 30 households (who have both pets and gardens)
- Ask students to observe and say what they see
Ask questions to guide:
- “Of the 80 households that have pets, how many also have gardens?”
- “So what is the probability that among the households that have pets, there is a garden?”
Formula Correspondence:
- Write the conditional probability formula: P(B|A) = P(A∩B)/P(A)
- A is “having a pet” and B is “having a garden”.
Identify the media you created and the tools you used.
For the video portion of this assignment, I used an iPad to record the video and imovie to edit the video. The video part is mainly responsible for explaining and analyzing the example problems to help students understand and master the knowledge more intuitively. At the same time, students can watch the video anytime and anywhere, and adjust the speed to help them learn.
Finally, I installed the H5P plugin in wordpress to create practice questions for the students. The type of questions I chose were multiple choice and added detailed comments and hints to each option to help students read and understand the questions. With these questions, I can test the students’ mastery of the basic rules, and the difficulty of the questions will keep increasing to help them consolidate their learning. The main reason I chose H5P is that it provides an interactive element, such as the multiple choice questions we used in this case. This interactive element can increase students’ engagement and motivation to learn and improve learning outcomes. At the same time, students can get instant feedback and correct answers to help them deepen their impressions.
Identify the principles, theories and techniques
Firstly, we have used the principle of coherence in the videos to ensure that there is no background music in the videos, only the human part, to ensure that other voices do not interfere with the students’ ability to watch the videos. In addition, I followed Voice, I always used real human voices in the videos instead of choosing to use AI-generated audio files to help students feel more immersed. Also, I adhered to the Segmenting principle in the production of the videos by making sure that each video was no longer than five minutes to ensure that the students would not be distracted by the length of the video, which would lead to a decrease in efficiency. Lastly, I used the Personalization Principle in the videos, and the overall feeling of the videos was relaxed and enthusiastic without giving the viewer an overly serious atmosphere. I also used the Personalization Principle in the video.
In addition to this, I also used the Image Principle in my Venn diagram design so that the students could understand the theorem of probability better. Also, I used Personalization Principle, at one minute and 05 seconds in the second video, I posed a question to the audience, ‘did you notice something’. It creates a relaxing and enjoyable learning atmosphere for the students and they will be curious and active to think about the question. These two parts make the students attracted to my course and ENGAGE in the course.
Lastly, I used a back design throughout the course with the content being distributed into big ideas, Learning Outcomes, Evidence of Learning, Assessments, and Learning Activities. The reason I chose the back design is because I was using the back design because I was talking about the math aspect of the course and I wanted to make sure that it was not too long. I am talking about math, and back design helps me to give my students clear learning objectives to start with, and then effectively plan instruction and assessments based on their math knowledge.
Determine what media you included from other sources and why you chose it
Youtube: Math Antics – Basic Probability
This video provides students with basic definitions and simple usage of concepts, which can help students learn the content of the course better and can be used by students as a pre-course study.
Textbook: Probability
This textbook is a very professional mathematical knowledge textbook, the explanation and ideas are systematic, structured and logical, can be used as a comprehensive guide to the concepts, the book has a large number of examples with answers and exercises to facilitate the application of knowledge.
Website: Probability formulas
This site provides a comprehensive compilation of probability formulas and sample problem analysis. Each probability theorem and formula includes clear explanations and examples so that readers can easily grasp the concepts. In addition, it contains the vast majority of conceptual formulas, and learners can quickly find the resources they need on the site. Finally, the resource is also helpful for students taking a probability course, as it provides a handy reference for basic concepts and problem-solving. For example, it provides calculations for common probability distributions and statistics.
Lesson plan
Big Idea:
- Conditional probability is an important tool for understanding the relationship between events. It helps us make reasonable predictions and decisions in the face of uncertainty.
Course Objectives:
- understand the definition and formula of conditional probability.
- distinguish between dependent and independent events
- 描述条件概率在现实生活中的应用
Learning outcomes:
- learn how to apply conditional probability to solve real-world problems (e.g., dice rolling, card drawing problems).
- distinguish between Dependent Events & Independent Events
- Describe at least one industry where probability is applied, explain how it is used in each, and explain the possible outcomes or benefits of the application.
Evidence of learning:
- correctly calculate conditional probability
- participate in exercises to apply what they have learned to solve real-life problems
Assessments:
- Two sets of in-class problems (one each on rolling dice and drawing cards) on conditional probability.
Learning activities:
Have students cut two large circles out of colored cardstock:
- The blue circle represents the 80 households that have pets
- The yellow circle represents the 50 households that have gardens
Draw a large box on the board to represent 120 households and have students come up to the table and place the two circles:
- The overlapping part of the two circles is 30 households (who have both pets and gardens)
- Ask students to observe and say what they see
Ask questions to guide:
- “Of the 80 households that have pets, how many also have gardens?”
- “So what is the probability that among the households that have pets, there is a garden?”
Formula Correspondence:
- Write the conditional probability formula: P(B|A) = P(A∩B)/P(A)
- A is “having a pet” and B is “having a garden”.
Reference:
DeMichele, Thomas. “Probability Theory Was Invented to Solve a Gambling Problem.” Fact or Myth?, factmyth.com, factmyth.com/factoids/probability-theory-was-invented-to-solve-a-gambling-problem. Accessed 29 Nov. 2024.
“History of Probability.” International Journal of Science and Research, www.ijsr.net/get_abstract.php?paper_id=ART20203456. Accessed 29 Nov. 2024.
Khan Academy. “Bayes Theorem.” YouTube, uploaded by Khan Academy, 20 Jan. 2021, https://www.youtube.com/watch?v=KzfWUEJjG18.
Pitman, Jim. Probability. Springer Science & Business Media, 2012.
“Probability.” Math is Fun, 2023, https://www.mathsisfun.com/data/probability.html. Accessed 30 Nov. 2024.
Comments are Disabled